Kali ini kita akan mempelajari tentang Bilangan Bulat. Apakah Bilangan Bulat jika kalian belum tahu baca artikel Penjumlahan dan Pengurangan Bilangan Bulat untuk lebih mengetahui dasar bilangan bulat.
Pengertian Pangkat Bilangan Bulat
24 = 2 x 2 x 2 x 2 (Cara membaca : 2 pangkat 4)
35 = 3 x 3 x 3 x 3 x 3 (Cara membaca : 3 pangkat 5)
46 = 4 x 4 x 4 x 4 x 4 x 4 (Cara membaca : 4 pangkat 6)
67 = 6 x 6 x 6 x 6 x 6 x 6 x 6 (Cara membaca : 6 pangkat 7)
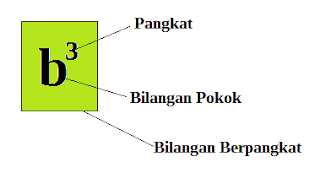
Bentuk b3 disebut bilangan berpangkat. Angka b disebut bilangan pokok atau bilangan dasar, sedangkan angka 3 disebut pangkat.
Untuk sembarang bilangan bulat a dan bilangan bulat positif m, berlaku
am = m x m x m x m x ..... x m.
m faktor
Contoh Soal :
Dengan cara menulis dalam bentuk perkalian faktor-faktornya, tentukan nilai berikut !
a. 54
b. (-6)3
Jawab :
a. 54 = 5 x 5 x 5 x 5 = 625
b. (-6)3 = (-6) x (-6) x (-6) = -216
1. Tulislah bentuk perkalian berikut menjadi bentuk pangkat !
a. 4 x 4 x 4
b. 8 x 8 x 8 x 8
c. k x k x k x k x k
d. (-2) x (-2) x (-2) x (-2)
2. Ubahlah bilangan berpangkat berikut menjadi bentuk perkalian berulang !
a. 46 d. (-5)5
b. 76 e. (-10)4
c. 98 f. (-k)7
3. Tentukan hasil perpangkatan berikut !
a. 43 c. 67 e. (-6)3
b. 37 d. (-3)5 f. (-8)4
4. Hitunglah nilai dari operasi berikut !
a. 33 x 3 + 5 x 32
b. 32 x 33 + 23 x 4
c. 52 x 5 - 23 x 42
d. (-3)3 x (-3)2 - (-2)3 x (-4)2
5. Pak Hendra mempunyai 6 bebek, masing-masing bebek mempunyai 6 anak. Masing-masing anak bebek mempunyai 6 anak bebek lagi. Berapakah jumlah bebek Pak Hendra?
6. Lambang * berarti pangkat duakan bilangan pertama. kemudian tambahkan hasilnya dengan bilangan kedua.
a. Hitunglah 4 * 6 dan 6 * 4.
b. Hitunglah 5 * (-1) dan (-1) * 7.
c. Apakah operasi * bersifat komutatif?
Menghitung Akar Kuadrat dan Akar Pangkat Tiga dari Bilangan Bulat.
1. Akar kuadrat adalah kebalikan (invers) dari operasi pangkat dua.
Contohnya lihat di bawah ini.
| 22 kebalikan √ | 2 | 42 kebalikan | √ | 16 |
| √ | 2 | kebalikan 22 | √ | 16 | kebalikan 42 |
2. Akar pangkat tiga adalah kebalikan (invers) dari operasi pangkat tiga.
| 23 kebalikan 3√ | 8 | 43 kebalikan 3 | √ | 64 |
| 3√ | 8 | kebalikan 23 3 | √ | 64 | kebalikan 43 |
Contoh Soal :
Tentukan akar kuadrat berikut ini.
| a. √ | 225 | b. | √ | 676 | c. 3 | √ | 3375 |
Jawab :
= 3 x 5 = 2 x 13
| √ | 225 | = | √ | 3 x 75 | b. | √ | 676 | = √ | 4 x 169 |
| = √ | 3 x 3 x 25 | = | √ | 4 x 13 x 13 |
| = √ | 32 x 52 | = | √ | 22 x 132 |
= 15 = 26
| c. ^3√ | 3.375 | = ^3 | √ | 5 x 676 |
| = ^3√ | 5 x 25 x 25 x 27 |
| = ^3√ | 53 x 33 |
| = ^3√ | 53 | x ^3 | √ | 33 |
= 15
Tips mengerjakan dengan mudah
1. Cari perpangkatan terendah berapa yang bisa dibagi dengan akar kuadrat yang memiliki nilai akhir akhir kuadrat dan hasil perpangkatan yang sama.
2. Bagikan akar kuadrat dengan perpangkatan dan lihat hasilnya apakah ada faktronya atau tidak.
3. Faktorkan semuanya kemudian dikali.
misalnya ;
Jawab:
| √ | 225 | = Angka Akhir 5 |
Mencari perpangkatan yang bisa dibagi, yaitu 52 = 25 (angka akhir 5)
| √ | 225 | bisa dibagi dengan 25 |
| Dibagikan dengan √ |
225
|
| √ |
225 : 25
| = | √ | 9 |
| √ | 9 | = 3 |
faktornya dikalikan
5 x 3 = 15
Contohnya jadi seperti ini
= 5 x 3
| √ | 225 | = 25 x 3 |
= 15
Untuk lebih memahami, kerjakanlah soal-soal di bawah ini;
1. Tentukan hasil operasi bilangan berikut!
| a. 63 h. √ |
49
|
| b. 73 i. √ |
81
|
| c. 83 j. 3√ |
216
|
| d. 263 k. √ |
7.392
|
| e. 903 l. √ |
9.025
|
| f. 2243 m. √ |
10.000
|
| g. 3183 n. √ |
13.225
|
2. Pak Andre memiliki bangunan rumah yang berbentuk persegi. Panjang sisi bangunan rumah tersebut 250 m. Berapa meter persegi luas bangunan rumah Pak Andre ?
3. Pak Arif akan bangunan rumah yang berbentuk persegi di pinggir jalan. Diketahui luas tanah itu 72.900 m3, tentukan
a. panjang sisi tanah;
b. keliling tanah tersebut.
4. Sebuah kandang kelinci berbentuk kubus dengan volume 1.728 m3. Tentukan panjang sisi kandang kelinci tersebut.
5. Reni memiliki sebatang kayu yang panjangnya 170 cm. Reni ingin membuat model kubus dari kayu tersebut tanpa sisa.
a. Berapa panjang sisi model kubus yang terbentuk?
b. Berapa volume model kubus yang terbentuk?
Sifat-Sifat Bilangan Berpangkat
a. Sifat Perkalian Bilangan Berpangkat
Jika m, n adalah bilangan bulat positif dan a bilangan bulat maka am x an = am + n.
Contoh Soal :
Dengan cara menuliskan dalam bentuk perkalian, tunjukkan bahwa 36 x 33 = 39!
Jawab:
36 x 33 = ( 3 x 3 x 3 x 3 x 3 x 3) x (3 x 3 x 3)
6 faktor 3 faktor
= (3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3)
(6 + 3) faktor
= 26 + 3
= 29
b. Sifat Pembagian Bilangan Berpangkat
Jika m, n bilangan bulat positif dan m > n dengan a bilangan bulat dan a bukan 0, maka am : an = am - n.
Contoh Soal :
Dengan cara menuliskan dalam bentuk perkalian, tunjukkan bahwa 36 : 33 = 33!
Jawab :
36 : 33 = 36
33
= (3 x 3 x 3 x 3 x 3 x 3)
3 x 3 x 3
= (3 x 3 x 3)
(6 - 3) faktor
= 36 - 3
= 33
c. Sifat Perpangkatan Bilangan Berpangkat
Jika a, m, dan n bilangan bulat maka (am)n = am x n.
Contoh Soal:
Dengan cara menuliskan dalam bentuk perkalian, tunjukkan bahwa (43)2 = 46.
Jawab:
(43)2 = (43) x (43)
= (4 x 4 x 4) x (4 x 4 x 4)
3 faktor 3 faktor
= 4 x 4 x 4 x 4 x 4 x 4
(3 x 2) faktor
= 43 x 2 = 46
d. Sifat Perpangkatan pada Perkalian
Jika a, b bilangan bulat dan m bilangan bulat positifmaka (a x b)m = am x bm.
Contoh Soal=
Dengan cara menuliskan dalam bentuk perkalian, tunjukkan bahwa (32)3 = 33 x 23.
Jawab:
(32)3 = (3 x 2) x (3 x 2) x (3 x 2)
= (3 x 3 x 3) x (2 x 2 x 2)
3 faktor 3 faktor
= 33 x 23
e. Sifat Perpangkatan pada Pembagian.
Jika a, b bilangan bulat (b bukan 0) dan m bilangan bulat positif, maka (a : b)m = am : bm.
Contoh soal:
Dengan cara menuliskan dalam bentuk pembagian, tunjukkan bahwa (5 : 3)4 = 54 : 34.
Jawab:
(5 : 3)4 = (5/3)4
= (5/3) x (5/3) x (5/3) X (5/3)
= (5 x 5 x 5 x 5) = 54 = 54 : 53
(3 x 3 x 3 x 3) 34
Untuk lebih memahami, kerjakanlah soal-soal di bawah ini!
Tentukan nilai perkalian, pembagian, dan perpangkatan berikut ini! (Kerjakan dengan kolkulator saja)
a. 33 x 32 f. 45 : 43
b. 65 x 62 g. 711 : 74
c. 46 x 44 h. (33)3
d. 63 x 66 i. (3 x 4)4
e. 314 x 39 j. (8 : 3)5
a. 33 x 32 f. 45 : 43
b. 65 x 62 g. 711 : 74
c. 46 x 44 h. (33)3
d. 63 x 66 i. (3 x 4)4
e. 314 x 39 j. (8 : 3)5














0 komentar:
Post a Comment